SICP - Solution: Exercise 1.14
October 9, 2018
Exercise 1.14 #
Draw the tree illustrating the process generated by the count-change procedure of 1.2.2 in making change for 11 cents. What are the orders of growth of the space and number of steps used by this process as the amount to be changed increases?
Solution #
By updating the call with display, it is possible to generate data in
GrapViz DOT format and plot it. The calls that match (= amount 0) are in darker gray.
digraph G {
node [color = gray95,style=filled];
graph [ranksep=0.25];
node [color = gray95,style=filled,fontsize=9,shape=box, margin=.08, width=0, height=0 ];
edge [penwidth=.5, arrowsize=0.5];
"[0] (cc 11 5)" [label="(cc 11 5)", ];
"[0] (cc 11 5)" -> "[1] (cc 11 4)"; "[1] (cc 11 4)" [label="(cc 11 4)", ];
"[1] (cc 11 4)" -> "[2] (cc 11 3)"; "[2] (cc 11 3)" [label="(cc 11 3)", ];
"[2] (cc 11 3)" -> "[3] (cc 11 2)"; "[3] (cc 11 2)" [label="(cc 11 2)", ];
"[3] (cc 11 2)" -> "[4] (cc 11 1)"; "[4] (cc 11 1)" [label="(cc 11 1)", ];
"[4] (cc 11 1)" -> "[5] (cc 11 0)"; "[5] (cc 11 0)" [label="(cc 11 0)", ];
"[4] (cc 11 1)" -> "[5] (cc 10 1)"; "[5] (cc 10 1)" [label="(cc 10 1)", ];
"[5] (cc 10 1)" -> "[6] (cc 10 0)"; "[6] (cc 10 0)" [label="(cc 10 0)", ];
"[5] (cc 10 1)" -> "[6] (cc 9 1)"; "[6] (cc 9 1)" [label="(cc 9 1)", ];
"[6] (cc 9 1)" -> "[7] (cc 9 0)"; "[7] (cc 9 0)" [label="(cc 9 0)", ];
"[6] (cc 9 1)" -> "[7] (cc 8 1)"; "[7] (cc 8 1)" [label="(cc 8 1)", ];
"[7] (cc 8 1)" -> "[8] (cc 8 0)"; "[8] (cc 8 0)" [label="(cc 8 0)", ];
"[7] (cc 8 1)" -> "[8] (cc 7 1)"; "[8] (cc 7 1)" [label="(cc 7 1)", ];
"[8] (cc 7 1)" -> "[9] (cc 7 0)"; "[9] (cc 7 0)" [label="(cc 7 0)", ];
"[8] (cc 7 1)" -> "[9] (cc 6 1)"; "[9] (cc 6 1)" [label="(cc 6 1)", ];
"[9] (cc 6 1)" -> "[10] (cc 6 0)"; "[10] (cc 6 0)" [label="(cc 6 0)", ];
"[9] (cc 6 1)" -> "[10] (cc 5 1)"; "[10] (cc 5 1)" [label="(cc 5 1)", ];
"[10] (cc 5 1)" -> "[11] (cc 5 0)"; "[11] (cc 5 0)" [label="(cc 5 0)", ];
"[10] (cc 5 1)" -> "[11] (cc 4 1)"; "[11] (cc 4 1)" [label="(cc 4 1)", ];
"[11] (cc 4 1)" -> "[12] (cc 4 0)"; "[12] (cc 4 0)" [label="(cc 4 0)", ];
"[11] (cc 4 1)" -> "[12] (cc 3 1)"; "[12] (cc 3 1)" [label="(cc 3 1)", ];
"[12] (cc 3 1)" -> "[13] (cc 3 0)"; "[13] (cc 3 0)" [label="(cc 3 0)", ];
"[12] (cc 3 1)" -> "[13] (cc 2 1)"; "[13] (cc 2 1)" [label="(cc 2 1)", ];
"[13] (cc 2 1)" -> "[14] (cc 2 0)"; "[14] (cc 2 0)" [label="(cc 2 0)", ];
"[13] (cc 2 1)" -> "[14] (cc 1 1)"; "[14] (cc 1 1)" [label="(cc 1 1)", ];
"[14] (cc 1 1)" -> "[15] (cc 1 0)"; "[15] (cc 1 0)" [label="(cc 1 0)", ];
"[14] (cc 1 1)" -> "[15] (cc 0 1)"; "[15] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[3] (cc 11 2)" -> "[4] (cc 6 2)"; "[4] (cc 6 2)" [label="(cc 6 2)", ];
"[4] (cc 6 2)" -> "[5] (cc 6 1)"; "[5] (cc 6 1)" [label="(cc 6 1)", ];
"[5] (cc 6 1)" -> "[6] (cc 6 0)"; "[6] (cc 6 0)" [label="(cc 6 0)", ];
"[5] (cc 6 1)" -> "[6] (cc 5 1)"; "[6] (cc 5 1)" [label="(cc 5 1)", ];
"[6] (cc 5 1)" -> "[7] (cc 5 0)"; "[7] (cc 5 0)" [label="(cc 5 0)", ];
"[6] (cc 5 1)" -> "[7] (cc 4 1)"; "[7] (cc 4 1)" [label="(cc 4 1)", ];
"[7] (cc 4 1)" -> "[8] (cc 4 0)"; "[8] (cc 4 0)" [label="(cc 4 0)", ];
"[7] (cc 4 1)" -> "[8] (cc 3 1)"; "[8] (cc 3 1)" [label="(cc 3 1)", ];
"[8] (cc 3 1)" -> "[9] (cc 3 0)"; "[9] (cc 3 0)" [label="(cc 3 0)", ];
"[8] (cc 3 1)" -> "[9] (cc 2 1)"; "[9] (cc 2 1)" [label="(cc 2 1)", ];
"[9] (cc 2 1)" -> "[10] (cc 2 0)"; "[10] (cc 2 0)" [label="(cc 2 0)", ];
"[9] (cc 2 1)" -> "[10] (cc 1 1)"; "[10] (cc 1 1)" [label="(cc 1 1)", ];
"[10] (cc 1 1)" -> "[11] (cc 1 0)"; "[11] (cc 1 0)" [label="(cc 1 0)", ];
"[10] (cc 1 1)" -> "[11] (cc 0 1)"; "[11] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[4] (cc 6 2)" -> "[5] (cc 1 2)"; "[5] (cc 1 2)" [label="(cc 1 2)", ];
"[5] (cc 1 2)" -> "[6] (cc 1 1)"; "[6] (cc 1 1)" [label="(cc 1 1)", ];
"[6] (cc 1 1)" -> "[7] (cc 1 0)"; "[7] (cc 1 0)" [label="(cc 1 0)", ];
"[6] (cc 1 1)" -> "[7] (cc 0 1)"; "[7] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[5] (cc 1 2)" -> "[6] (cc -4 2)"; "[6] (cc -4 2)" [label="(cc -4 2)", ];
"[2] (cc 11 3)" -> "[3] (cc 1 3)"; "[3] (cc 1 3)" [label="(cc 1 3)", ];
"[3] (cc 1 3)" -> "[4] (cc 1 2)"; "[4] (cc 1 2)" [label="(cc 1 2)", ];
"[4] (cc 1 2)" -> "[5] (cc 1 1)"; "[5] (cc 1 1)" [label="(cc 1 1)", ];
"[5] (cc 1 1)" -> "[6] (cc 1 0)"; "[6] (cc 1 0)" [label="(cc 1 0)", ];
"[5] (cc 1 1)" -> "[6] (cc 0 1)"; "[6] (cc 0 1)" [label="(cc 0 1)",color=gray80];
"[4] (cc 1 2)" -> "[5] (cc -4 2)"; "[5] (cc -4 2)" [label="(cc -4 2)", ];
"[3] (cc 1 3)" -> "[4] (cc -9 3)"; "[4] (cc -9 3)" [label="(cc -9 3)", ];
"[1] (cc 11 4)" -> "[2] (cc -14 4)"; "[2] (cc -14 4)" [label="(cc -14 4)", ];
"[0] (cc 11 5)" -> "[1] (cc -39 5)"; "[1] (cc -39 5)" [label="(cc -39 5)", ];
}
Coins value #
Since some of us might not be familiar with the values of US coins, here is a quick reference:
| Kind of Coin | Coin Name | Coin Value |
|---|---|---|
| 1 | 1 penny | 1 cent |
| 2 | 1 nickel | 5 cents |
| 3 | 1 dime | 10 cents |
| 4 | 1 quarter | 25 cents |
| 5 | 1 half-dollar | 50 cents |
Orders of growth of space #
Since this is a recursive process, the orders of growth of the space will be proportional to the depth of the tree.
It is easy to see that the longest series of calls will happen when making the change of the amount n using only pennies (1 cent). The order of growth of space for cc will be $\mathrm\Theta(n)$
Orders of growth of the number of steps #
For estimating the orders of growth of the number of steps, we focus on counting the number of calls to cc.
The first step is to get an intuitive understanding of the shape of the growth by exploring low dimension solutions that we can plot. Let’s start with graphing the shape of the trees when using only pennies for (cc 6 1).
digraph G {
node [color = gray95,style=filled];
graph [ranksep=0.3,size=7];
node [color = gray95,style=filled,fontsize=9,shape=box, margin=.08, width=0, height=0 ];
edge [penwidth=.1, arrowsize=0.5];
"[0] (cc 6 1)" [label="(cc 6 1)",color=lightblue];
"[0] (cc 6 1)" -> "[1] (cc 6 0)"; "[1] (cc 6 0)" [label="(cc 6 0)", ];
"[0] (cc 6 1)" -> "[1] (cc 5 1)"; "[1] (cc 5 1)" [label="(cc 5 1)",color=lightblue];
"[1] (cc 5 1)" -> "[2] (cc 5 0)"; "[2] (cc 5 0)" [label="(cc 5 0)", ];
"[1] (cc 5 1)" -> "[2] (cc 4 1)"; "[2] (cc 4 1)" [label="(cc 4 1)",color=lightblue];
"[2] (cc 4 1)" -> "[3] (cc 4 0)"; "[3] (cc 4 0)" [label="(cc 4 0)", ];
"[2] (cc 4 1)" -> "[3] (cc 3 1)"; "[3] (cc 3 1)" [label="(cc 3 1)",color=lightblue];
"[3] (cc 3 1)" -> "[4] (cc 3 0)"; "[4] (cc 3 0)" [label="(cc 3 0)", ];
"[3] (cc 3 1)" -> "[4] (cc 2 1)"; "[4] (cc 2 1)" [label="(cc 2 1)",color=lightblue];
"[4] (cc 2 1)" -> "[5] (cc 2 0)"; "[5] (cc 2 0)" [label="(cc 2 0)", ];
"[4] (cc 2 1)" -> "[5] (cc 1 1)"; "[5] (cc 1 1)" [label="(cc 1 1)",color=lightblue];
"[5] (cc 1 1)" -> "[6] (cc 1 0)"; "[6] (cc 1 0)" [label="(cc 1 0)", ];
"[5] (cc 1 1)" -> "[6] (cc 0 1)"; "[6] (cc 0 1)" [label="(cc 0 1)",color=gray80];
}
Colors in this chart indicate the number of kinds-of-coins.
The process here is linear and every node is splitting into two substeps, but only the node with (cc x 1) will recurse deeper. All the (cc x 0) are leaves of this tree since it indicates that there is no more type of coins to use.
From this graph we notice that:
- There are 6 blue nodes from
(cc 6 1)to(cc 1 1), which will recurse after using the last type of coin. - There are 6 gray nodes from
(cc 6 0)to(cc 1 0), which won’t recurse because this is the case where(= kinds-of-coins 0). - There is one dark gray node
(cc 0 1)with a amount of 0, indicating a solution.
If $T(n,m)$ is the number of call to cc for amount $n$ and $m$ type of coin, we can see that:
$$T(6,1)=2\times6+1$$
From there, we can generalize to any amount $m$ when using only pennies:
$$T(n,1)=2n+1$$
Let’s go one step further by exploring how things work with two kinds of coins: pennies (1 cent) and nickels (5 cents). By drawing the tree for (cc 12 2), and arranging the nodes a little, we see that we have a neat 2 dimensional array:
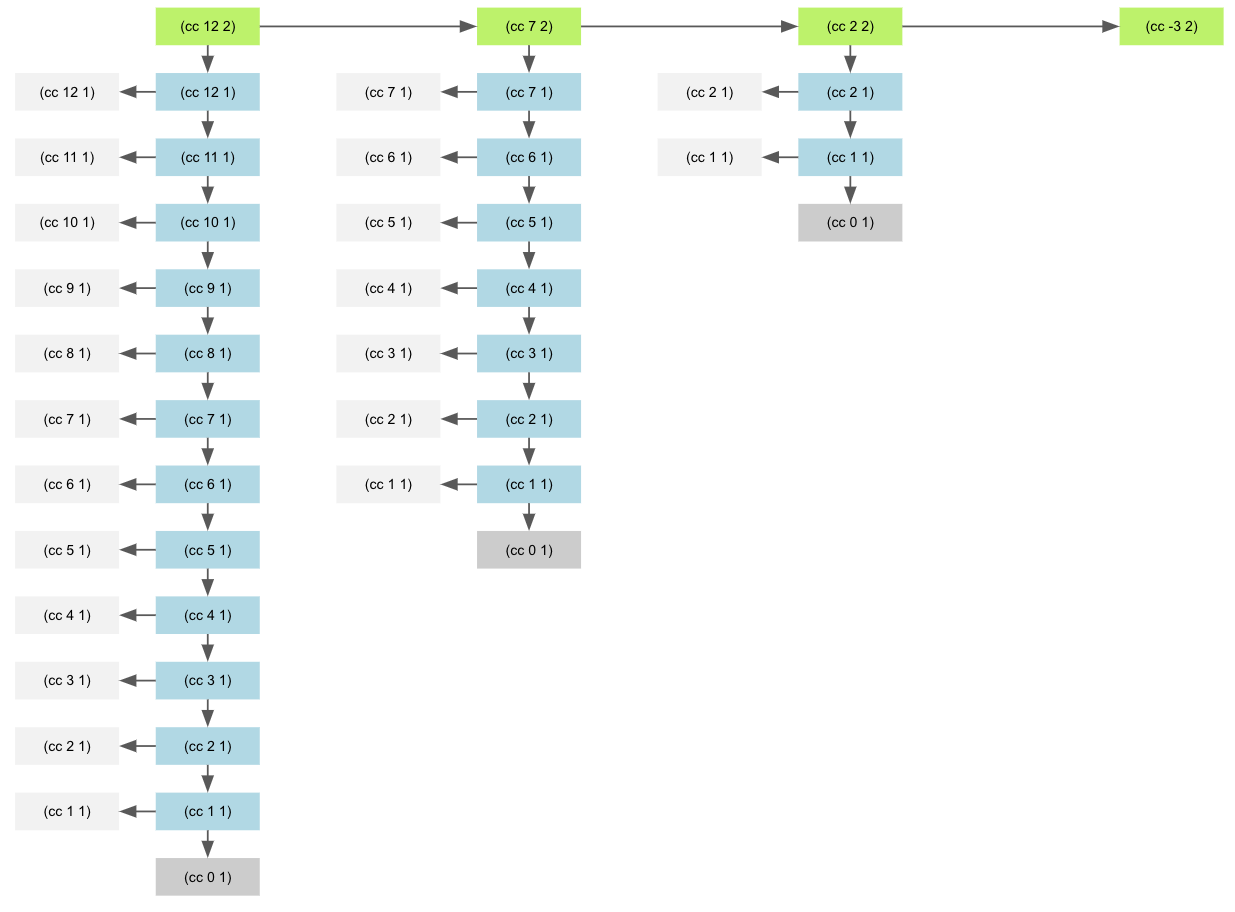
Let’s break it down:
- There are 4 green nodes for
(cc x 2), corresponding to how many times you can subtract a nickel (5 cents) from 12, plus one. - Then for each of the green node, the path below corresponds to the option of using only pennies, which is the case that we looked at first.
For an amount $n$, there is at most $Floor\left(\frac n5\right)+1$ times you can subtract a nickel (5 cents) before reaching zero or a negative value. By simplifying a little, and ignoring the floor that won’t impact, the result when the number grows larger, it is possible to estimate the number of calls to cc as $T(n,2)$ which are composed of two parts:
- There is $\frac n5+1$ green nodes.
- for each green node, there is a node for pennies that start from the value $n$.
We can rewrite this as an equation and simplify it:
$$T(n,2) =\frac n5+1+ \sum_{i=0}^{n/5}T(n-5i,1)$$
$$T(n,2) =\frac n5+1+ \sum_{i=0}^{n/5}(2n-10i+1)$$
$$T(n,2) =\frac n5+1+\frac{2n^2}5+\frac n5-10 \sum_{i=0}^{n/5}i$$
$$T(n,2) =\frac n5+1+\frac{2n^2}5+\frac n5-10\frac{{\displaystyle\frac n5}\left({\displaystyle\frac n5}+1\right)}2$$
$$T(n,2)=\frac n5+1+\frac{2n^2}5+\frac n5-n\left(\frac n5+1\right)$$
$$T(n,2)=\frac n5+1+\frac{2n^2}5+\frac n5-\frac{n^2}5-n$$
$$T(n,2) =\frac{2n}5+\frac{2n^2}5-\frac{n^2}5-n+1$$
Very interestingly, it is possible to define a function that gives the exact number of steps for a given number $n$:
$$T(n,2) =\frac{n^2-3n}5+1$$
Which means that for two types of coins, the order of growth of the number of steps is:
$$T(n,2) =\mathrm\Theta(n^2)$$
For $T(n,3)$:
$$T(n,3) =\frac n{10}+1+ \sum_{i=0}^{n/10}T(n-10i,2)$$
if you take the trouble to expand the equation, you will find that:
$$T(n,3) =\mathrm\Theta(n^3)$$
by continuing to apply the formulas:
$$T(n,3) =\frac n{10}+1+ \sum_{i=0}^{n/10}T(n-10i,2)$$
$$T(n,4) =\frac n{25}+1+ \sum_{i=0}^{n/25}T(n-25i,3)$$
$$T(n,5) =\frac n{50}+1+ \sum_{i=0}^{n/50}T(n-50i,4)$$
By doing all the expansion, you find that the order of growth of the number of steps is:
$$T(n,5) =\mathrm\Theta(n^5)$$
Overall, this is not only a very slow process, it is also a very inefficient way to implement this computation, because the same computation is repeated many times. You can have a look at the solution for this exercise by Sarabander here to see how to implement the solution in only $n^2$.